The last couple of R. L. Deppmann Monday Morning Minutes introduced the BTUH corrections required when using glycol in hydronic heating and cooling systems. Today we look at the friction loss in pipes when using ethylene or propylene glycols instead of water.
The 2017 Fundamentals handbook from the American Society of Heating, Refrigeration, and Air Conditioning Engineers (ASHRAE) uses Bernoulli’s Equation to define the friction loss in piping systems. The friction loss depends on a few variables with one of them being the density of the fluid. We understand that the density of a water/glycol mixture is different than 100% water. This difference can make a huge difference when calculating the pump head required. Let’s look at the Bell & Gossett System Syzer to see how much of a difference there is.
Bell & Gossett System Syzer Pressure Drop Calculator
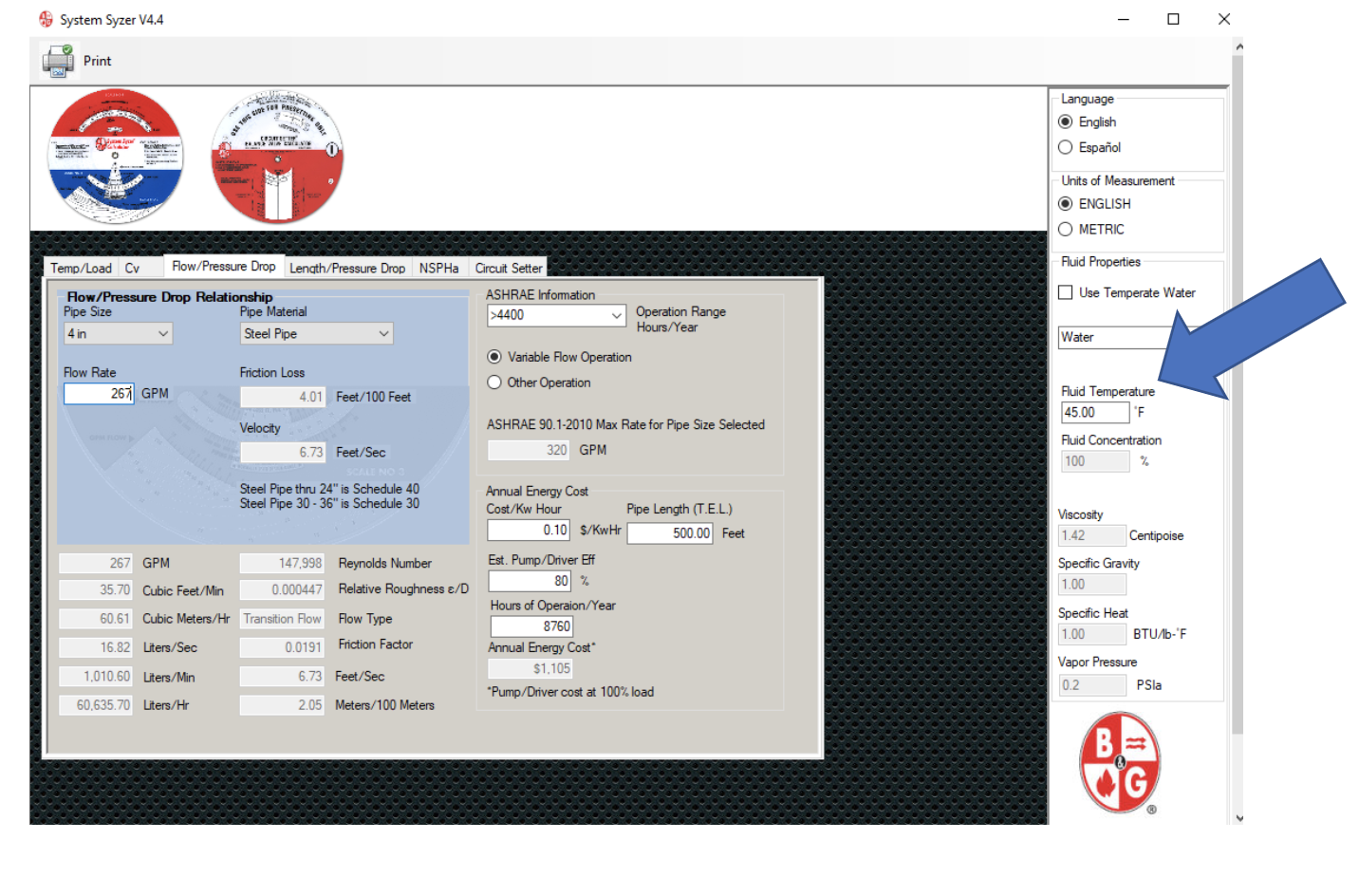
Let’s look at an example system using 267 GPM of water in 4” steel pipe. The system is chilled water with a supply temperature of 40°F and a return of 50°F. What is the friction loss in the pipe?
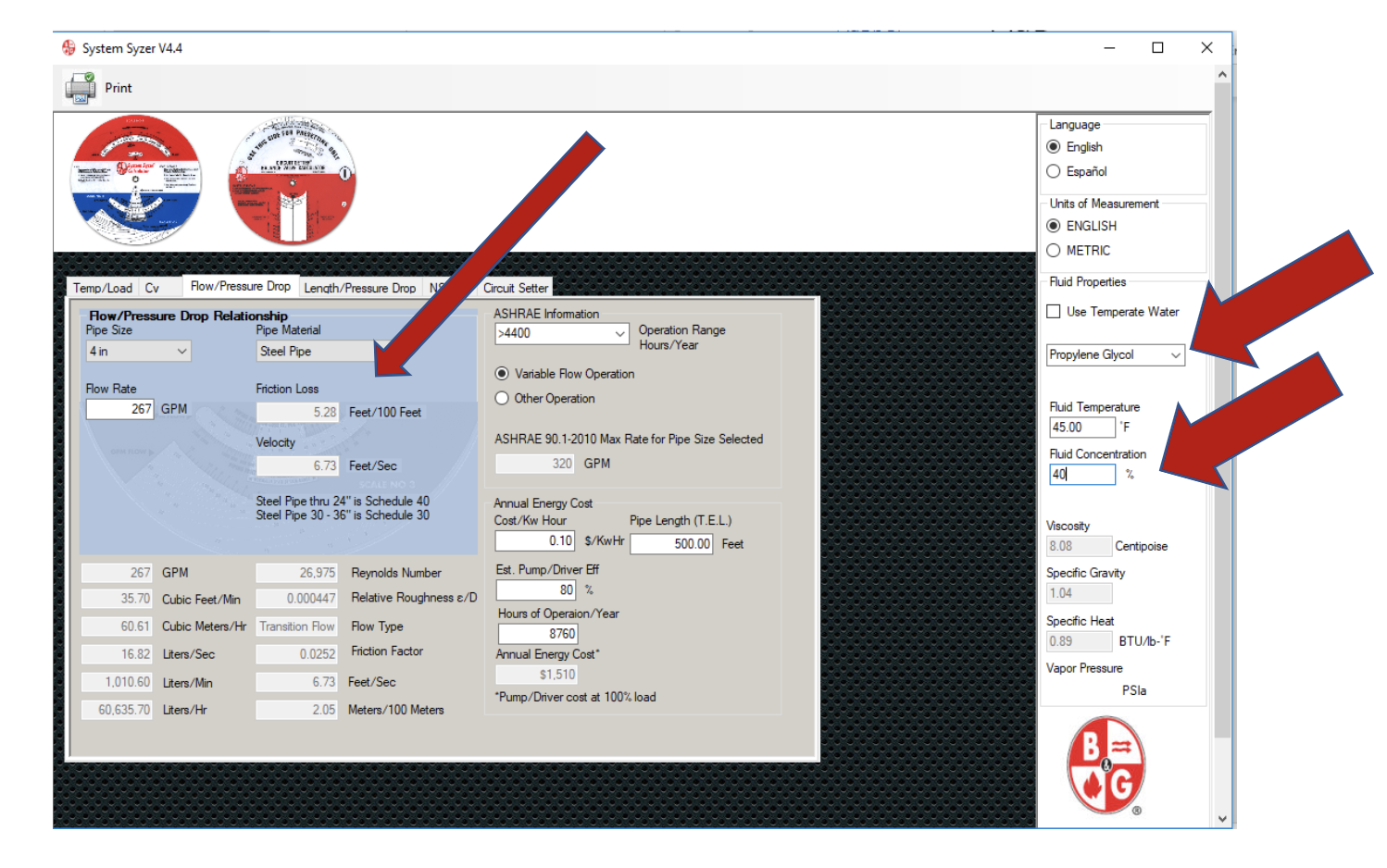
Notice I have changed the fluid temperature for the water. The friction loss is 4.01 feet of pressure drop per 100 feet of pipe. What happens if we change to a 40% propylene glycol (PG) solution?
This would be a real issue if we missed this in the calculations! The friction loss changed to 5.28 feet per hundred of loss. This is a 32% increase in friction. There is even more to be concerned about. In the September 23rd R. L. Deppmann Monday Morning Minute, I indicated the need to change the flow rate from 267 GPM to 284 GPM to get the same heat transfer load we had when the system used water only. If we change the flow rate to 284 GPM in that 4’ pipe, the friction loss will once again increase and will be 5.90 feet per hundred. This is another 11% increase over the 32% increase. Not something we want to miss.
Pump Curves and Flow Rate if we miss the Glycol Corrections
We cannot use the 4” pipe correction as a universal correction since the velocity and Reynolds number also affects the change in friction loss. That said, it is close enough for this example. Let’s assume the pump was selected for 267 GPM at 80 feet of head but the engineer forgot the glycol corrections. What will happen when the balance contractor reads the pump at the design temperatures? If we assume the correction factor of 5.90/4.01 = 47% for the entire 80 feet and correct the flow rate, we will now need 284 GPM at 117 feet.
The water selection below shows a 9.375” impeller and a 10 HP motor with a brake horsepower (BHP) at design of 7.21 HP. The pump would be variable speed, but we will just show the constant speed curve for clarity. What would the pump look like?
Propylene Glycol Needs More Horsepower than Water
Glycol is heavier than water at this temperature. If I start by keeping the 267 GPM at 80 feet selection and change from water to 40% PG, there is a pump correction. It takes more horsepower to move the glycol than water. The water HP shown above is 7.21. Just changing to glycol and keeping the same capacities results in BHP increasing to 7.84 HP. That is an increase of almost 9% before we even change capacities. Now let’s look when we correct the pump requirement to 284 GPM at 117 feet.
The red curve above is the system curve for the new capacities. The pump will only be able to produce 225 GPM of 40% PG at 45°F. If this was a variable speed pump, could we Overspeed it and make up the difference? To get the 284 GPM, we would have to speed up the pump to 2894 RPM. This is well above the manufacturer’s suggested maximum of 120% of speed. In addition, the 10 HP motor would be too small. We would need a 15 HP motor for the design. This is a no-win mistake.
Remember to always correct the flow and head for fluids other than water. Also, remember to indicate the required fluid and temperature used on the pump curve. It may make a difference in horsepower!